Hace algunos dias en
www.gaussianos.com aparecia el post que os dejo a continuacion.
El maravilloso
teorema de la Bola Peluda, es un resultado que se suele ilustrar diciendo que es imposible
peinar
una bola que esté completamente cubierta de pelo. Ya se habló en
Gaussianos hace un tiempo acerca de él, y hoy vamos a volver a hacerlo.
Y vamos a volver a hacerlo gracias a
Dani, que hace un
tiempo me envió una interesante demostración de este resultado traducida
y preparada casi para publicarla. Y hoy va a ser el día en que aparezca
en el blog.

El
resultado en realidad es más general y afirma que no existe ningún
campo continuo de vectores tangentes (que siempre sean distintos de
cero) en ninguna esfera de dimensión par. Existen multitud de
demostraciones de este hecho, en su mayoría bastante complicadas, que
usan argumentos combinatorios, de teoría homológica o homotópica, de
formas diferenciales o incluso de topología geométrica, pero en 1978 el
genio de la topología diferencial
John Milnor,
premio Abel en 2011, publicó una demostración de este teorema que es completamente elemental.
Es cierto que a pesar de no necesitar maquinaria pesada es un texto
matemático hecho y derecho que posiblemente asuste a algunos, pero
realmente la idea que hay detrás es simplemente, en palabras del propio
Milnor,
“la observación de que la función  no es un polinomio para
no es un polinomio para  impar”
impar”.
La prueba sólo requiere conocimientos básicos de cálculo en varias
variables y algo de familiaridad con la topología general, y es una
pincelada de elegancia que nos ofrece el hombre que recibió una medalla
Fields en 1959 por su descubrimiento de las
esferas exóticas: espacios topológicos de dimensión 7 que eran homeomorfos a la 7-esfera

pero no difeomorfos. Dicho de otra manera, dotó a la 7-esfera de
estructuras diferenciables no equivalentes a la usual. El estudio de las
esferas exóticas aún está lejos de estar cerrado, y de hecho no se sabe
si existen estructuras diferenciables exóticas en la esfera de
dimensión 4.
Teorema de la bola peluda…y demostración
Bueno, entremos ya en materia. Vamos a comenzar volviendo a enunciar el teorema:
Teorema de la bola peluda
Ninguna esfera de dimensión par admite un campo continuo de vectores tangentes que no se anule en ningún punto.
La esfera de dimensión

, denotada por
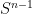
, se define como el subconjunto de vectores

del espacio euclideo

que tienen norma

igual a 1 (y llamaremos

al conjunto de vectores con norma

). Un vector

se dice
tangente a
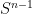
en

si el producto escalar euclideo
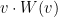
es cero.
Por supuesto que un campo tangente en la esfera sería simplemente una aplicación
para la cual
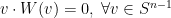
.
Decimos que es un campo
continuo si sus funciones coordenadas son continuas y que es
suave
si todas tienen derivadas parciales continuas de todos los órdenes. La
restricción de que el campo no se anule en ningún punto simplemente se
traduce en exigir

.
También es importante darse cuenta de que la restricción sobre la paridad de la dimensión es esencial. En la esfera

podemos definir el campo
que claramente cumple las condiciones pedidas. También notamos que si
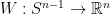
es un campo de vectores continuo y tangente que nunca se anula, el campo

es un campo continuo y tangente que además es unitario. Bastará por lo
tanto probar que no existen campos continuos, tangentes y unitarios.
Nosotros demostraremos el Teorema con la hipótesis adicional de suavidad
del campo. El caso general se puede deducir de éste con el
Teorema de Aproximación de Weierstrass,
que permite aproximar cualquier función continua por una polinómica (y
por lo tanto infinitamente diferenciable) haciendo el error tan pequeño
como queramos. De esta forma bastará comprobar la veracidad del
siguiente hecho:
Ninguna esfera de dimensión par admite un campo
suave de vectores tangentes y unitarios.
Procedamos con la demostración de esta última afirmación:
Sea
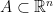
una región compacta y
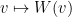
un campo suave que está definido en un entorno de

. Consideremos para cada número real

la aplicación

que hace
Esta última aplicación está definida en todo

, y entonces es fácil demostrar el primer Lema que necesitaremos:
Lema 1:
Si el parámetro  es suficientemente pequeño, la aplicación
es suficientemente pequeño, la aplicación  es inyectiva y transforma la región
es inyectiva y transforma la región  en una región cercana
en una región cercana  , cuyo volumen se puede expresar como un polinomio en
, cuyo volumen se puede expresar como un polinomio en  .
.
La primera afirmación se sigue del hecho de que una aplicación
continuamente diferenciable definida en un compacto es Lipschitz, esto
es, existe una constante

tal que para cualesquiera

se tiene que
Para quien no sepa cómo demostrar esto, comentar que es simplemente
la aplicación el teorema del valor medio en cada coordenada. A partir de
esto vemos que si fuera
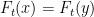
, se tendría

, y por lo tanto la desigualdad
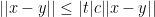
obliga a que sea

si se tiene

.
En estas condiciones sabemos que el volumen de la región

se puede calcular mediante la integral
Pero la diferencial de

tiene una matriz jacobiana en

de la forma
por lo que su determinante será de la forma
para ciertas funciones

definidas en

. En particular, para

pequeño será estrictamente positivo y podemos escribir la anterior integral como
donde
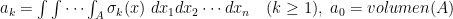
.
Esto demuestra el primer Lema. Para completar la prueba necesitaremos
otro más. Supongamos, para buscar una contradicción, que existe un
campo suave de vectores tangentes y unitarios
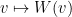
definido en una esfera de dimensión par

. Consideramos nuestra región

como la región compacta que yace entre dos esferas concéntricas

y
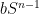
de radios

, y extendemos el campo
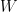
a todo

por la ecuación

para cada

. Así

es un campo de vectores definido en todo

que por el Teorema de Pitágoras lleva la esfera unidad dentro de la esfera de radio

.
Lema 2:
Si el parámetro  es suficientemente pequeño,
es suficientemente pequeño,  lleva la esfera
lleva la esfera 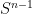 en la esfera de radio
en la esfera de radio  de manera sobreyectiva.
de manera sobreyectiva.
Suponemos sin problemas
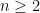
. El determinante de la diferencial de

, que vimos que era de la forma

, no se anula para

pequeño. Así pues, por el Teorema de la Función Inversa, lleva abiertos del interior de

a abiertos de

. En particular, la imagen

es un conjunto relativamente abierto de la esfera de radio

. Pero como

es también compacto, y por lo tanto cerrado, es un subconjunto del espacio conexo

que es a la vez abierto y cerrado, de modo que por no ser vacío ha de ser el total.
Estamos ya en condiciones de concluir la demostración del Teorema de
la Bola Peluda. En efecto, se sigue del segundo Lema que para cada

, la aplicación

lleva la esfera

de manera sobreyectiva en la esfera de radio
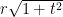
, y por lo tanto

es la región concéntrica entre las esferas de radios

y
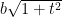
. Pero es obvio entonces que podemos expresar el volumen de esta región por la fórmula
que para

impar no es un polinomio en

, una contradicción con el primer Lema.

Milnor también es reconocido en la comunidad matemática por redactar
sus textos de una manera extremadamente clara e intuitiva. Recomiendo a
cualquiera que quiera aprender las ideas que yacen detrás de la
topología diferencial su libro
Topology from the Differentiable Viewpoint.
En 50 páginas mete una cantidad de conceptos e ideas increíble, y no
requiere más conocimientos que esta demostración. Es fantástico.



 El
resultado en realidad es más general y afirma que no existe ningún
campo continuo de vectores tangentes (que siempre sean distintos de
cero) en ninguna esfera de dimensión par. Existen multitud de
demostraciones de este hecho, en su mayoría bastante complicadas, que
usan argumentos combinatorios, de teoría homológica o homotópica, de
formas diferenciales o incluso de topología geométrica, pero en 1978 el
genio de la topología diferencial John Milnor,
El
resultado en realidad es más general y afirma que no existe ningún
campo continuo de vectores tangentes (que siempre sean distintos de
cero) en ninguna esfera de dimensión par. Existen multitud de
demostraciones de este hecho, en su mayoría bastante complicadas, que
usan argumentos combinatorios, de teoría homológica o homotópica, de
formas diferenciales o incluso de topología geométrica, pero en 1978 el
genio de la topología diferencial John Milnor,