Matematicas y software libre: abril 2012

Canonical ha anunciado la disponibilidad de Ubuntu 12.04 LTS Precise Pangolin, una nueva edición de esta popular distribución que llega con cambios destacables en diversos apartados.

En las notas de la versión podéis encontrar la descripción de esas novedades de las que ya hemos hablado en el pasado, tales como la integración de HUD (Heads-Up Display) en Unity, las opciones de personalización de Unity gracias a las preferencias del sistema y a la inclusión de MyUnity o el soporte extendido de touchpads, incluidos la mayoría de Synaptics y de los trackpads de los portátiles de Apple.

En materia de apliaciones se ha elegido a Rythmbox como aplicación de reproducción musical por defecto, en la cual está integrada la Ubuntu One Music Store. LibreOffice está en versión 3.5.2, mientras que contamos con GNOME3.4.1 como entorno de escritorio, lo que hará sencillo instalar la nueva versión de GNOME Shell y las aplicaciones que se han retocado especialmente en esa versión de GNOME, tales como Epiphany (“Web”) o Boxes, el gestor de virtualización.

Hay más novedades que podéis comprobar en el anuncio oficial, y por supuesto ya podéis descargar e instalar Ubuntu 12.04 LTS Precise Pangolin en diversos formatos desde este enlace.

Hace algunos dias en www.gaussianos.com aparecia el post que os dejo a continuacion.
El maravilloso teorema de la Bola Peluda, es un resultado que se suele ilustrar diciendo que es imposible peinar una bola que esté completamente cubierta de pelo. Ya se habló en Gaussianos hace un tiempo acerca de él, y hoy vamos a volver a hacerlo.

Y vamos a volver a hacerlo gracias a Dani, que hace un tiempo me envió una interesante demostración de este resultado traducida y preparada casi para publicarla. Y hoy va a ser el día en que aparezca en el blog.
John Milnor

El resultado en realidad es más general y afirma que no existe ningún campo continuo de vectores tangentes (que siempre sean distintos de cero) en ninguna esfera de dimensión par. Existen multitud de demostraciones de este hecho, en su mayoría bastante complicadas, que usan argumentos combinatorios, de teoría homológica o homotópica, de formas diferenciales o incluso de topología geométrica, pero en 1978 el genio de la topología diferencial John Milnor, premio Abel en 2011, publicó una demostración de este teorema que es completamente elemental.
Es cierto que a pesar de no necesitar maquinaria pesada es un texto matemático hecho y derecho que posiblemente asuste a algunos, pero realmente la idea que hay detrás es simplemente, en palabras del propio Milnor, “la observación de que la función $(1+t^2)^{n/2}$ no es un polinomio para $n$ impar”. La prueba sólo requiere conocimientos básicos de cálculo en varias variables y algo de familiaridad con la topología general, y es una pincelada de elegancia que nos ofrece el hombre que recibió una medalla Fields en 1959 por su descubrimiento de las esferas exóticas: espacios topológicos de dimensión 7 que eran homeomorfos a la 7-esfera $S^7$ pero no difeomorfos. Dicho de otra manera, dotó a la 7-esfera de estructuras diferenciables no equivalentes a la usual. El estudio de las esferas exóticas aún está lejos de estar cerrado, y de hecho no se sabe si existen estructuras diferenciables exóticas en la esfera de dimensión 4.

Teorema de la bola peluda…y demostración

Bueno, entremos ya en materia. Vamos a comenzar volviendo a enunciar el teorema:

Teorema de la bola peluda
Ninguna esfera de dimensión par admite un campo continuo de vectores tangentes que no se anule en ningún punto.

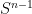
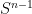
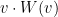
La esfera de dimensión $n-1$ , denotada por $S^{n-1}$ , se define como el subconjunto de vectores $v=(v_1,v_2,\ldots,v_n)$ del espacio euclideo $\mathbb{R}^n$ que tienen norma $||v||$ igual a 1 (y llamaremos $rS^{n-1}$ al conjunto de vectores con norma $r$ ). Un vector $W(v)\in \mathbb{R}^n$ se dice tangente a $S^{n-1}$ en $v$ si el producto escalar euclideo $v \cdot W(v)$ es cero.
Por supuesto que un campo tangente en la esfera sería simplemente una aplicación

$W:S^{n-1} \rightarrow \mathbb{R}^n$

para la cual $v \cdot W(v)=0, \; \forall v \in S^{n-1}$ .
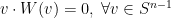
Decimos que es un campo continuo si sus funciones coordenadas son continuas y que es suave si todas tienen derivadas parciales continuas de todos los órdenes. La restricción de que el campo no se anule en ningún punto simplemente se traduce en exigir $W(v)\neq 0 \quad \forall v \in S^{n-1}$ .
También es importante darse cuenta de que la restricción sobre la paridad de la dimensión es esencial. En la esfera $S^{2n-1} \subset \mathbb{R}^{2n}$ podemos definir el campo

$W(v_1,v_2,\ldots,v_{2n})=(v_2,-v_1,\ldots,v_{2n},-v_{2n-1})$

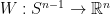
que claramente cumple las condiciones pedidas. También notamos que si $W:S^{n-1} \rightarrow \mathbb{R}^n$ es un campo de vectores continuo y tangente que nunca se anula, el campo $v \mapsto \frac{W(v)}{||W(v)||}$ es un campo continuo y tangente que además es unitario. Bastará por lo tanto probar que no existen campos continuos, tangentes y unitarios. Nosotros demostraremos el Teorema con la hipótesis adicional de suavidad del campo. El caso general se puede deducir de éste con el Teorema de Aproximación de Weierstrass, que permite aproximar cualquier función continua por una polinómica (y por lo tanto infinitamente diferenciable) haciendo el error tan pequeño como queramos. De esta forma bastará comprobar la veracidad del siguiente hecho:

Ninguna esfera de dimensión par admite un campo
suave de vectores tangentes y unitarios.

Procedamos con la demostración de esta última afirmación:
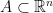
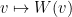
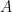
Sea $A\subset \mathbb{R}^n$ una región compacta y $v \mapsto W(v)$ un campo suave que está definido en un entorno de $A$ . Consideremos para cada número real $t$ la aplicación $F_t$ que hace

$F_t(v)=v+tW(v)$

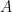
Esta última aplicación está definida en todo $A$ , y entonces es fácil demostrar el primer Lema que necesitaremos:

Lema 1:
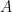Si el parámetro $t$ es suficientemente pequeño, la aplicación $F_t$ es inyectiva y transforma la región $A$ en una región cercana $F_t(A)$ , cuyo volumen se puede expresar como un polinomio en $t$ .

La primera afirmación se sigue del hecho de que una aplicación continuamente diferenciable definida en un compacto es Lipschitz, esto es, existe una constante $c > 0$ tal que para cualesquiera $x,y \in A$ se tiene que

$|| W(x)-W(y) || \leq c|| x-y||$

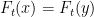
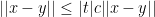
Para quien no sepa cómo demostrar esto, comentar que es simplemente la aplicación el teorema del valor medio en cada coordenada. A partir de esto vemos que si fuera $F_t(x)=F_t(y)$ , se tendría $x-y=t(W(x)-W(y))$ , y por lo tanto la desigualdad $||x-y|| \leq |t|c ||x-y||$ obliga a que sea $x=y$ si se tiene $|t| < 1/c$ .
En estas condiciones sabemos que el volumen de la región $F_t(A)$ se puede calcular mediante la integral

$\displaystyle{volumen(F_t(A))= \int \int \cdots \int_{A} |det[ d(F_t)_x ]| \, \, dx_1dx_2\cdots dx_n }$

Pero la diferencial de $F_t$ tiene una matriz jacobiana en $x \in A$ de la forma

$d(F_t)_x=Id_n + t(dW_x)$

por lo que su determinante será de la forma

$1+\sigma_1(x) t + \cdots + \sigma_n(x)t^n$

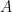
para ciertas funciones $\sigma_k=\sigma_k(x)$ definidas en $A$ . En particular, para $t$ pequeño será estrictamente positivo y podemos escribir la anterior integral como

$\displaystyle{volumen (F_t(A))=\int \int \cdots \int_{A} |det[ d(F_t)_x ]| \, \, dx_1dx_2\cdots dx_n=a_0 + a_1t+ \cdots +a_nt^n}$

donde $a_k= \int \int \cdots \int_{A} \sigma_k(x) \, \, dx_1dx_2\cdots dx_n \quad (k\geq1), \; a_0=volumen(A)$ .
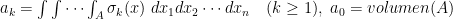
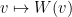
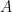
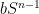
Esto demuestra el primer Lema. Para completar la prueba necesitaremos otro más. Supongamos, para buscar una contradicción, que existe un campo suave de vectores tangentes y unitarios $v \mapsto W(v)$ definido en una esfera de dimensión par $S^{n-1}$ . 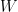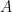Consideramos nuestra región $A$ como la región compacta que yace entre dos esferas concéntricas $aS^{n-1}$ y $bS^{n-1}$ de radios $a < 1 < b$ , y extendemos el campo $W$ a todo $A$ por la ecuación $W(u)=||u||W(\frac{u}{||u||})$ para cada $u \in A$ . 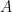Así $F_t(u)=u+tW(u)$ es un campo de vectores definido en todo $A$ que por el Teorema de Pitágoras lleva la esfera unidad dentro de la esfera de radio $\sqrt{1+t^2}$ .

Lema 2:
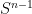Si el parámetro $t$ es suficientemente pequeño, $F_t$ lleva la esfera $S^{n-1}$ en la esfera de radio $\sqrt{1+t^2}$ de manera sobreyectiva.

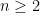
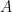
Suponemos sin problemas $n \geq 2$ . El determinante de la diferencial de $F_t$ , que vimos que era de la forma $1+\sigma_1(x) t + \cdots + \sigma_n(x)t^n$ , no se anula para $t$ pequeño. Así pues, por el Teorema de la Función Inversa, lleva abiertos del interior de $A$ a abiertos de $\mathbb{R}^n$ . En particular, la imagen $F_t(S^{n-1})$ es un conjunto relativamente abierto de la esfera de radio $\sqrt{1+t^2}$ . Pero como $F_t(S^{n-1})$ es también compacto, y por lo tanto cerrado, es un subconjunto del espacio conexo $\sqrt{1+t^2}\,S^{n-1}$ que es a la vez abierto y cerrado, de modo que por no ser vacío ha de ser el total.
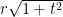
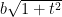
Estamos ya en condiciones de concluir la demostración del Teorema de la Bola Peluda. En efecto, se sigue del segundo Lema que para cada $r \in (a,b)$ , la aplicación $F_t$ lleva la esfera $r S^{n-1}$ de manera sobreyectiva en la esfera de radio $r\sqrt{1+t^2}$ , y por lo tanto $F_t(A)$ es la región concéntrica entre las esferas de radios $a\sqrt{1+t^2}$ y $b\sqrt{1+t^2}$ . Pero es obvio entonces que podemos expresar el volumen de esta región por la fórmula

$volumen(F_t(A))=(1+t^2)^{n/2}\,\,volumen(A)$

que para $n$ impar no es un polinomio en $t$ , una contradicción con el primer Lema. $\Box$
Milnor también es reconocido en la comunidad matemática por redactar sus textos de una manera extremadamente clara e intuitiva. Recomiendo a cualquiera que quiera aprender las ideas que yacen detrás de la topología diferencial su libro Topology from the Differentiable Viewpoint. En 50 páginas mete una cantidad de conceptos e ideas increíble, y no requiere más conocimientos que esta demostración. Es fantástico.

jueves, 26 de abril de 2012

Ubuntu 12.04 LTS disponible.

martes, 24 de abril de 2012

Ubuntu 12.10 Quantal Quetzal: adios al marron en Ubuntu.

lunes, 23 de abril de 2012

Una demostracion de Milnor del teorema de la bola peluda.

Teorema de la bola peluda…y demostración

Ninguna esfera de dimensión par admite un campo
suave de vectores tangentes y unitarios.

jueves, 26 de abril de 2012

Ubuntu 12.04 LTS disponible.

martes, 24 de abril de 2012

Ubuntu 12.10 Quantal Quetzal: adios al marron en Ubuntu.

lunes, 23 de abril de 2012

Una demostracion de Milnor del teorema de la bola peluda.

Teorema de la bola peluda…y demostración

Ninguna esfera de dimensión par admite un campo suave de vectores tangentes y unitarios.

Ninguna esfera de dimensión par admite un campo
suave de vectores tangentes y unitarios.