Matematicas y software libre: ¿Como cazaria un matematico a un leon?

¿Cómo cazaría un matemático a un león en el desierto del Sahara? La misma pregunta se la hizo H. Pétard, de Princeton, Nueva Jersey, y propuso el siguiente método (entre otros).

Método de Bolzano-Weierstrass. Bisecamos el desierto con una cerca de norte a sur. El león se encontrará en la parte este o en la parte oeste; suponemos que en la parte oeste. Bisecamos esta parte con una cerca de este a oeste. El león se encontrará en la parte norte o en la parte sur; suponemos que en la parte norte. Continuamos este proceso indefinidamente, construyendo una cerca lo suficientemente fuerte alrededor de cada una de las partes seleccionadas en cada paso. El diámetro de las partes tiende a cero, por lo que el león terminará rodeado por una cerca de diámetro arbitrariamente pequeño.

Este y otros métodos aparecen en el artículo A contribution to the mathematicasl theory of big game hunting, aparecido en el American Mathematical Monthly, 45 (1938), pp. 446-447 (pueden ver un PDF aquí). H Pétard es pseudónimo de los matemáticos Ralph P. Boas Jr., en ese entonces postdoc de Salomon Bochner en la Universidad de Princeton, y Frank Smithies, profesor de la Universidad de Cambridge y buen amigo de Boas mientras estuvo de visita en Princeton. El artículo fue el resultado de chistes matemáticos producidos en varias parrandas.
El método recibe el nombre de “Bolzano-Weierstrass” por la demostración del teorema del mismo nombre, en honor de los matemáticos Bernard Bolzano (1781-1848) y Karl Weierstrass (1815-1897), y del cual hablaremos esta semana.
El protagonista del análisis matemático es el límite: una sucesión de números $a_1, a_2, a_3, ...$ tiene el límite $L$ , y escribimos $a_n\to L,$ si los elementos de la sucesión se acercan “arbitrariamente” a $L$ si avanzamos “suficientemente” en la lista. En términos precisos, para cualquier número positivo, llamémosle $\varepsilon,$ la diferencia entre $a_n$ y $L$ es menor que $\varepsilon$ si $n$ es suficientemente grande: existe $N$ tal que,

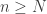si $n\ge N$ , entonces $|a_n - L| < \varepsilon$ .

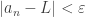Por ejemplo, la sucesión $\dfrac{1}{n} \to 0$ , mientras que las sucesiones $1, 2, 3, 4, \ldots$ o $0,1,0,1,0,\ldots$ no tienen límite.
Sin embargo, en la última de éstas, si tomamos solo los términos pares de la sucesión, entonces obtenemos $1, 1, 1, \ldots$ , la cual sí converge, obviamente a 1. Decimos entonces que la sucesión $0,1,0,1,\ldots$ tiene una subsucesión convergente.
En general, una subsucesión de $a_1, a_2, a_3, \ldots$ es una sucesión $a_{n_1}, a_{n_2}, a_{n_3}, \ldots$ con $n_1 < n_2 < n_3 < \cdots$ . Es decir, es una sucesión formada con términos de la sucesión original, distintos y en el mismo orden. Con “distintos” nos referimos al índice de la sucesión (la posición de los términos en la lista), no a los valores de los términos en sí. En el ejemplo anterior, la subsucesión $1, 1, 1, \ldots$ de $0,1,0,1,\ldots$ corresponde a los términos pares de la sucesión: $a_2, a_4, a_6, \ldots$ .
Es claro que la sucesión $1, 2, 3, 4, \ldots$ no tiene subsucesiones convergentes, porque todos sus términos crecen indefinidamente. ¿Cuándo podemos garantizar que una sucesión tiene subsucesiones convegentes? El teorema de Bolzano-Weierstrass nos da la respuesta.

Teorema (Bolzano-Weierstrass). Si la sucesión $a_1, a_2, a_3, \ldots$ es acotada, entonces tiene una subsucesión convergente.

Decimos que una sucesión es acotada si todos los valores de sus términos pertenecen a un intervalo, digamos, $[A,B]$ ; es decir, $a_n \in [A,B]$ para todo $n$ . A los números $A$ y $B$ los llamamos cotas de la sucesión.
Así, $0,1,0,1,\ldots$ es acotada porque sus términos se encuentran dentro de $[0,1]$ (o $[-2,2]$ , o cualquier otro intervalo donde se encuentren los números 0 y 1), mientras que $1, 2, 3, 4, \ldots$ no lo es.
La demostración del teorema de Bolzano-Weierstrass se lleva a cabo por el método de cacería descrito al inicio de esta entrada: bisecamos el intervalo $[A,B]$ y consideramos los intervalos $[A, \frac{A+B}{2}]$ y $[\frac{A+B}{2}, B].$ Como todos los términos de la sucesión se encuentran en $[A,B]$ y son infinitos (otra vez, nos referimos a los índices de los términos, y no a los valores, que podrían ser finitos y repetirse inifinitamente, como en nuestro ejemplo del 0 y 1), entonces uno de los dos subintervalos $[A, \frac{A+B}{2}]$ o $[\frac{A+B}{2}, B]$ debe contener una infinidad de ellos.
Si $[A, \frac{A+B}{2}]$ tiene una infinidad de términos de la sucesión, entonces hacemos $A_1 = A$ y $B_1 = \frac{A+B}{2}$ ; de otra forma, $A_1 = \frac{A+B}{2}$ y $B_1 = B.$ Siguiente, bisecamos $[A_1, B_1]$ , y tomamos uno de los intervalos $[A_1, \frac{A_1+B_1}{2}]$ o $[\frac{A_1+B_1}{2}, B_1]$ que tenga infinitos términos de la sucesión para obtener $[A_2, B_2].$ Continuamos de la misma forma para obtener una sucesión de intervalos cerrados $[A_n, B_n]$ tales que

Cada $[A_n, B_n]$ tiene una infinidad de términos de la sucesión $a_1, a_2, a_3, \ldots.$
Cada intervalo está contenido en el anterior: $[A_{n+1},B_{n+1}]\subset[A_n,B_n].$
La longitud de cada intervalo $[A_n, B_n]$ está dada por $B_n - A_n = \dfrac{B-A}{2^n}.$

Ahora bien, construimos una subsucesión de la siguiente forma: tomamos $a_{n_1}\in[A_1, B_1]$ ; luego, tomamos $a_{n_2}$ de tal forma que $n_2>n_1$ y $a_{n_2}\in[A_2,B_2].$ Esto es posible porque $[A_2, B_2]$ contiene una infinidad de términos de la sucesión. Repetimos el proceso: una vez tomados $a_{n_1}, \ldots, a_{n_k},$ tomamos $n_{k+1}>n_k$ tal que $a_{n_{k+1}}\in[A_{k+1},B_{k+1}].$
Observamos ahora que, si el número $x\in \bigcap_n [A_n,B_n]$ (es decir, está en todo intervalo $[A_n,B_n]$ )¹, entonces

$|a_{n_k} - x| \le \dfrac{B-A}{2^k} \to 0,$

por lo que $a_{n_k} \to x$ . Hemos encontrado una subsucesión convergente, lo que termina la demostración del teorema.
Es claro cómo podemos extender el teorema a sucesiones en $\mathbb R^n$ , en cualquier dimensión. El teorema de Bolzano-Weierstrass es indispensable en la teoría de funciones de varias variables, en la teoría de variable compleja y, en general, en todo el análisis.
La idea de subsucesiones convergentes es muy útil para entender, además, la teoría de operadores en espacios de dimensión infinita (como el espacio de funciones continuas, o el de funciones integrables), aún cuando es posible encontrar en tales espacios sucesiones acotadas sin subsucesiones convergentes. Los conjuntos (dentro de espacios métricos) cuyas sucesiones siempre tienen subsucesiones convergentes son llamados compactos, y saber cuándo un conjunto es compacto es importante para entender sus funciones continuas.

martes, 13 de marzo de 2012

¿Como cazaria un matematico a un leon?

No hay comentarios:

Publicar un comentario